Automata Finito no Determinista(NFDA)

 Un AFN se define como una 5-tupla (Q, Σ, q₀, δ, F) donde:

·         Q  es un conjunto de estados

·         Σ es un alfabeto donde se puede incluir al elemento nulo

·         Q₀ Є Q, donde Q₀ es el estado inicial

·         δ: Q x Σ ->Q donde q es una función de transición

·         F Є Q , donde F es un conjunto de estados Finales

donde P(Q) es el conjunto potencia de Q. Esto significa que los autómatas finitos deterministas son un caso particular de los no deterministas, puesto que Q pertenece al conjunto P(Q).
La interpretación que se suele hacer en el cómputo de un AFND es que el automáta  puede tener desde 0 hasta N tranciones con cuaquier simbolo incluyendo el simbolo Є o λ el cual nos indica una trancicion con caracter vacio.Asimismo, en un autómata finito no determinista podemos aceptar la existencia de más de un nodo inicial.

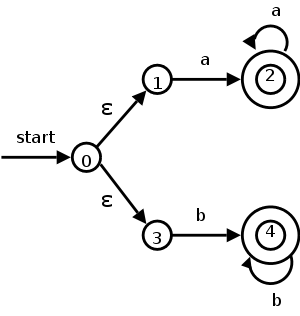
En la imagen de abajo se muestra un NFDA de ejemplo en donde vemos dos tranciones con Є

Ejercicio:

Obtenga el NFDA a partir de la tabla de transiciones y la gramática.

	a	b	ε
Q0	-	-	Q1 Q2
Q1	Q3	-	-
Q2	Q2 Q4	-	-
Q3	Q5	Q3	-
Q4	-	Q5	-
Q5	-		-

Una posible resultado

https://mega.co.nz/#!JBth2I4C!lNJB1aUIomtT5TRfOCgEiT1P9b5H-v-Tnwcb6FAfjjc



A partir de la siguiente gramática obtenga la tabla de transiciones y el grafo:


A=1,1, (0,1)*